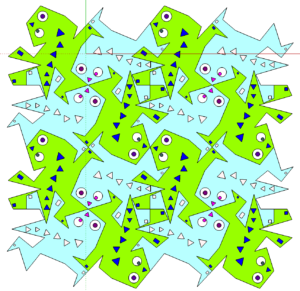
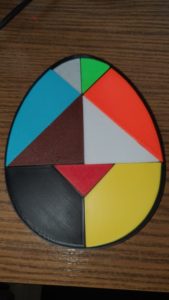
Escher Eidechsen

Die Schüler*innen bauen das Puzzle zunächst in Kleingruppen und dann als Klasse zusammen.
Anschließend wird die Zeichenebene mit Hilfe eines bereits vorgefertigten Angabeobjekts in einer CAD-Software parkettiert.
Vertiefend können wie im Anleitungsvideo eigene Escher-Figuren entworfen werden.
In dieser ergänzenden Dokumentation erfährt man, wie MC Escher zwischen den Welten der Geometrie und der Kunst wandelte. Für die Schüler*innen der Unterstufe ist nur der Trailer geeignet.
Zusammenfassung siehe PDF-Datei